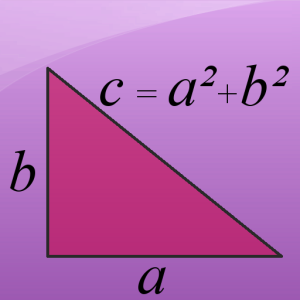<!doctype html>
قضیهٔ فیثاغورث — تعریف، برهانها و مثالهای حلشده
خلاصه: در مثلث قائمالزاویه مربع وتر برابر مجموع مربعهای دو ضلع دیگر است.
تعریف رسمی
اگر مثلثی قائمالزاویه باشد و دو ضلعهای قائمه را a و b و وتر (ضلع روبهروی زاویهٔ قائمه) را c بنامیم، آنگاه:
a2+b2=c2
یا بهصورت نمادین: a² + b² = c²
چرا مهم است؟
- قضیهٔ پایهای در هندسه اقلیدسی است و در حل مسائل طول، فاصله و مختصات کاربرد دارد.
- پایهٔ تعریف فاصلهٔ اقلیدسی در دستگاه مختصات کارتزین است.
چند برهان مشهور
۱) برهان با استفاده از شباهت مثلثها
این برهان یکی از تمیزترین برهانهاست. اگر مثلث اصلی را با وتر c و قائمهها a و b در نظر بگیریم و از رأس زاویهٔ قائمه به وتر، ارتفاعی رسم کنیم، آن ارتفاع مثلث را به دو مثلث کوچک تقسیم میکند که هر دو با مثلث بزرگ همشکل (مشابه) هستند. نسبتهای همشکلی منجر به برابر شدن a²+b² با c² میشود.
۲) برهان جبری (برهان با مختصات)
مثلث قائمالزاویهای را در دستگاه مختصات قرار میدهیم: نقاط را مثلاً (0,0)، (a,0) و (0,b) قرار میدهیم. فاصله بین (a,0) و (0,b) (که وتر است) از فرمول فاصله بهدست میآید:
c = √[(a-0)² + (0-b)²] = √(a² + b²) ⇒ c² = a² + b²
۳) برهان هندسی با بازآرایی (rearrangement)
در این برهان چهار مثلث قائمالزاویهٔ همشکل کنار هم در یک مربع قرار میگیرند؛ با دو نوع چینش مختلف میتوان مساحت فضای درون مربع مرکزی را همارز گرفته و معادلهٔ موردنظر را نتیجه گرفت (روش محبوب در نمایشهای تصویری).
۴) برهان اقلیدسی کلاسیک
در کتابهای قدیمی هندسه برهانهایی هندسی وجود دارد که با مقاطع مربعات روی اضلاع و دلایل متشابهت و مساحت این مربعات نشان میدهد مجموع مساحت دو مربع کوچک برابر مربع بزرگ است.
مثالهای عددی و حل گامبهگام
مثال ۱ — پیدا کردن وتر
اگر در مثلث قائمهای اضلاع قائمه برابر a = 3 و b = 4 باشند، مقدار وتر c چقدر است؟
حل:
a² + b² = c²
3² + 4² = c²
9 + 16 = c²
25 = c²
c = √25 = 5
پس وتر برابر 5 است.
مثال ۲ — پیدا کردن یکی از اضلاع قائمه
در مثلثی وتر برابر 13 و یکی از اضلاع قائمه برابر 5 است. ضلع دیگر چقدر است؟
حل:
a² + b² = c²
5² + b² = 13²
25 + b² = 169
b² = 169 - 25 = 144
b = √144 = 12
بنابراین ضلع دیگر برابر 12 است.
کاربردها و نکات تکمیلی
- محاسبهٔ فاصلهٔ بین دو نقطه در صفحهٔ دوبعدی (فرمول فاصله برگرفته از فیثاغورث است).
- در مثلثات برای رابطهٔ بین سینوس/کوسینوس و تبدیلهای هندسی کاربرد دارد.
- فیثاغورث برای پیدا کردن جذر مقادیر بزرگ کاربرد عملی در مهندسی و معماری دارد.
نکته: قضیهٔ فیثاغورث تنها در هندسهٔ اقلیدسی برقرار است؛ در هندسههای کروی یا هذلولوی روابط دیگری وجود دارند.
خلاصه و جمعبندی
قضیهٔ فیثاغورث میگوید در هر مثلث قائمالزاویه رابطهٔ a² + b² = c² برقرار است. این قضیه دارای برهانهای متنوع هندسی و جبری است و مفاهیم پایهای در هندسه و کاربردهای علمی را شکل میدهد.