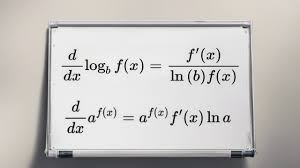تعریف اولیه مشتق

مشتق تابع \(f\) در نقطه \(a\) برابر است با حد نسبت تغییر مقدار تابع نسبت به تغییر متغیر، اگر این حد وجود داشته باشد:

f'(a) = lim_{h→0} (f(a + h) - f(a)) / h

این تعریف بیان می‌کند که هنگامی که تغییر کوچک \(h\) به صفر میل می‌کند، نسبت تغییر مقدار تابع به تغییر متغیر به چه عددی نزدیک می‌شود؛ آن عدد همان مشتق در آن نقطه است.

معنی هندسی مشتق

از نظر هندسی، مشتق در یک نقطه برابر شیب خط مماس بر نمودار تابع در همان نقطه است.

مثال

برای تابع \(f(x)=x^2\):

f'(x) = lim_{h→0} ((x+h)^2 - x^2) / h
       = lim_{h→0} (2xh + h^2) / h
       = lim_{h→0} (2x + h)
       = 2x